国际象棋界对丑闻并不陌生。近期备受关注的一则争议事件发生在 2023 年 11 月:克拉姆尼克在其chess.com博客及一段 YouTube 视频中暗示,中村光在一场快棋锦标赛中取得 45.5/50 的战绩时存在作弊行为。克拉姆尼克指出,中村光取得这一连胜的概率从统计学角度来看极低。不过,一个研究团队采用贝叶斯分析方法,并结合历史比赛表现数据进行研究后发现,中村光没有作弊的概率高达 99.6%。

本文探讨了有关美国国际象棋特级大师中村光在 2023 年一场线上快棋锦标赛中作弊的指控 —— 在该赛事中,中村光创下了 46 场比赛获 45.5 分的惊人连胜纪录。前世界冠军克拉姆尼克对相关统计证据提出质疑,该证据显示,若未作弊,这样的连胜几乎不可能实现;但由希瓦・马哈拉杰、波尔森和瓦迪姆・索科洛夫领衔的研究团队通过贝叶斯分析结合历史表现数据发现,中村光未作弊的概率高达 99.6%。
研究人员考虑了中村光相对于对手的实力差距后发现,仅从等级分概率来看,这样的连胜发生概率不足 3%;但贝叶斯分析在纳入估算的作弊发生率(线上比赛中低至万分之一)后显示,中村光清白的可能性极高 —— 概率高达 99.6%。
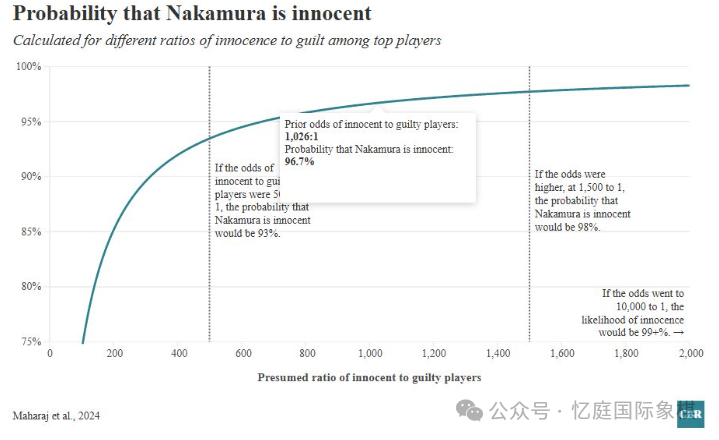
分析结果凸显了初始假设的重要性 —— 如果作弊行为的发生率远高于实际,清白的概率会下降,但仍会保持在较高水平(当作弊发生率为 1/1500 时,清白概率约为 98%)。
克拉姆尼克的论点是 “检察官谬误” 的典型例子:他将连胜的稀有性与有罪证据混为一谈,而事实上,一个概率极低的事件并不等同于存在不当行为。该文章警示了 “选择性筛选数据” 的问题,并强调需遵循 “似然原理”;结论应仅基于观察到的证据,而非取决于某些数据被突出展示的方式或原因。
文中还提及了 “克伦威尔法则”,提醒读者在概率分析中切勿赋予绝对确定性(即 0% 或 100% 的概率),因为未知因素始终可能存在。
研究得出结论:中村光的连胜最合理的解释是他卓越的技艺,以及一种真实存在但极为罕见的统计现象,而非作弊行为。文章呼吁对统计证据进行审慎、批判性的解读,避免因有缺陷的推理损害他人声誉。
统计陷阱
结论
注:文章转自忆庭国际象棋公众号